[315]
Stéphane Laurens * et Serge MOSCOVICI **
Respectivement maître de conférences, Université de Rennes II, Renne, France
et directeur d’études, EHESS, Paris, France
“La construction des échelles.”
In ouvrage sous la direction de Serge Moscovici et Fabrice Buschini, Les méthodes des sciences humaines, pp. 315-344. Paris : Les Presses universitaires de France, 2003, 472 pp.
 1. La matière pensante et parlante [315] 1. La matière pensante et parlante [315]
- 1.1. Propositions et attitudes [315]
- 1.2. Interpréter et mesurer [316]
- 2. Échelles nominales et échelles ordinales [318]
- 2.1. Échelles nominales [318]
- 2.1.1. Propriétés des échelles nominales [319]
- 2.2. Échelles ordinales [320]
- 2.2.1. Propriétés des échelles ordinales [321]
- 3. Les échelles de distance sociale [322]
- 4. Les Échelles de Thurstone pour la mesure des attitudes [324]
- 4.1. La méthode de comparaison par paires [325]
- 4.2 La méthode des intervalles a priori égaux [328]
- 5. L'échelle de Lickert [332]
- 6. La méthode de dépliage [333]
- 7. L'analyse hiérarchique [335]
- 7.1. Établissement des énoncés [339]
- 7.2. Établissement de l'échelle [339]
- 7.3. Évaluation de l’échelle [341]
- Conclusion [342]
- Références bibliographiques [343]
1. La matière pensante et parlante
- 1.1. Propositions et attitudes

Quand on considère, de la façon la plus large et la plus ouverte, un groupe, une société, il est malaisé de mettre en doute que chaque individu possède un fonds de connaissances et d'idées qui composent le vivier de toutes ses pensées, de tous ses choix. Il les retrouve au moment d'une rencontre avec les autres, un moment où se fait sentir le besoin de communiquer ou d'agir. Et chaque fois, il puise dans ce fonds pour scruter ses idées et ses connaissances, leur donner une forme acceptable à ses propres yeux et à ceux d'autrui. Elles sont en réalité mystérieuses et pourtant familières, d'autant plus irrésistibles que, toujours libres du point de vue de chacun, elles s'imposent néanmoins comme un langage ou un savoir commun. Il arrive à l'individu d'y penser volontairement, à titre de souvenirs et d'expériences personnelles, comme si elles avaient leur source dans l'existence de chacun. Mais à leur origine - habituellement, elles se ramènent à quelques grands thèmes - se trouve le plus souvent, on le sait, le groupe ou la société. Telle est leur ambiguïté : en tant que souvenirs ou expériences, leur contenu mental, leur sens commencerait seulement à exister à partir de ce que chacun possède en commun avec les autres.
On pourrait discuter à l'infini ce que nous entendons par « idée », « connaissance », « sens commun ». Des exemples se présentent à l'esprit de tous pour illustrer cette matière à penser et à parler devant laquelle nous nous trouvons en tant que psychologues sociaux et à partir de laquelle nous commençons nos recherches. On s'aperçoit qu'une « proposition » qui exprime ce savoir n'est pas simple : elle est extrêmement complexe. Des choix s'effectuent entre les propositions suivant des critères que l'on dirait capricieux, s'il n'y avait l'évidente régularité et la cohérence qui nous poussent [316] à croire qu'en eux se concentre l'essence même de notre vie psychique et sociale. Pourquoi justement ces choix et non pas d'autres ? De toute évidence, en face d'une proposition, nous exprimons ce qu'on peut appeler une « attitude » envers les objets ou les représentations que chacune des propositions dénote. Certaines attitudes sont parfois indiquées par des indices grammaticaux, en particulier les verbes.
Mais le plus souvent les attitudes, par exemple le désir, vis-à-vis d'un énoncé, sont rendues par des moyens lexicaux : « Je souhaite que le racisme disparaisse dans le monde. » On arrive donc à ce fait curieux : on étudie souvent les attitudes par rapport à un objet sans prêter attention à celles adoptées dans les énoncés les concernant. Songez à la question imaginaire suivante : « Êtes-vous pour ou contre la diffusion des organismes génétiquement modifiés dans l'agriculture française ? » À bien y réfléchir, on se demande quelle est l'attitude véritable des personnes qui répondent, par exemple, « pour ». Est-ce un désir (elles souhaitent cette diffusion), est-ce une volonté (elles veulent la diffusion) ou est-ce une croyance ?
L'étonnant est bien que l'on prétend évaluer une attitude, mais on ne sait pas laquelle. Ceci se ramène à cela : pour étudier toute cette matière pensante, parlante, il nous faut tenir compte de ces deux éléments : l'énoncé ou la proposition, et les attitudes telles que croyance, désir, etc., vis-à-vis de celui ou de celle-ci. Plus exactement, les attitudes propositionnelles.
- 1.2. Interpréter et mesurer

Dans ce qui précède, il ne s'agit, à vrai dire, que d'un moyen en vue d'une fin. Cette fin n'est atteinte que lorsqu'on a expliqué un phénomène ou un champ de phénomènes. Ces explications peuvent prendre des formes diverses. Chacune se propose d'élucider ou de rendre intelligible quelque chose, de nous aider à saisir ce que nous désirons comprendre. Un procédé qui nous est familier pour expliquer consiste à décomposer : des événements ou des phénomènes complexes deviennent plus accessibles, une fois que nous savons comment leurs différentes parties se rapportent et s'articulent les unes aux autres. Prenons l'exemple de la conformité : on reconnaît d'abord qu'il y a une opinion de la majorité et que celle-ci est inculquée à chaque membre de façon autoritaire, donc ils se conforment. Une façon tout à fait différente de comprendre un domaine de phénomènes consiste à concevoir une description claire de la structure de ce domaine. À cette fin, on fait se chevaucher ce domaine avec un autre dont on a auparavant élucidé la structure. Nous utilisons des temps de réaction calibrés et des machines psycho-galvaniques pour décrire la vitesse d'une réponse ou l'intensité d'une émotion. De même, nous comprenons la disposition de la surface de l'espace où nous vivons en le quadrillant par un système de coordonnées qui nous permet de spécifier des zones, d'évaluer des distances et de repérer l'emplacement des objets par rapport à d'autres.
Pour faire le point sur cette question, disons que la première forme d'explication s'efforce de saisir la manière dont opèrent une proposition et l'attitude de croyance, de désir, etc., vis-à-vis de son contenu, donc de déterminer pourquoi elles interagissent entre elles et avec leur environnement de façon à produire un résultat d'une espèce particulière. Car les représentations sous-jacentes à ces attitudes propositionnelles [317] jouent, en principe, un rôle causal. La seconde forme d'explication présuppose un cas particulier de mesure, l'application du domaine des nombres à un domaine d'objets sociaux. La structure des systèmes coordonnés de propositions et d'attitudes concernant les objets auxquels elles se réfèrent constitue ce que l'on appelle une échelle. Il existe des échelles relatives à toutes sortes de phénomènes, opinions, attitudes, représentations sociales, préjugés, et ainsi de suite. On peut concevoir qu'elles sont un moyen plus scientifique, plus précis, donc meilleur, d'étudier ce genre de phénomènes. Comment pourrait-il en être autrement, puisqu'elles quantifient ? En réalité, il s'agit d'une manière différente de comprendre, d'expliquer la matière parlante et pensante. Elle consiste à saisir par la mesure ce que l'on peut obtenir autrement par l'interprétation, chacune de ces démarches ayant sa propre logique. En tout cas, puisque l'on cherche à mesurer, il convient d'appliquer certaines règles à la mise en forme de cette matière, donc à ses grilles de lecture et aux questionnaires qui le permettent. Les voici :
- 1/ Les propositions doivent être courtes et ne pas excéder vingt mots.
- 2/ Les mots composant une proposition doivent être simples, clairs et directs.
- 3/ Chaque proposition doit se rapporter à une seule représentation dans la société.
- 4/ En règle générale, les propositions doivent être simples plutôt que mises sous forme de phrases composées et complexes.
- 5/ Les attitudes vis-à-vis des propositions doivent être tout à fait spécifiques, en évitant des mots tels que « pour », « contre » et d'autres tout aussi vagues.
- 6/ Il faut distinguer les propositions relatives à une connaissance ancienne de celles relatives à une connaissance nouvelle à propos de l'objet considéré.
- 7/ Distinguer nettement les jugements « absolus », plus tranchés, des jugements comparatifs, plus fins, concernant les objets étudiés.
- 8/ Il est souhaitable de référer l'objet considéré à son contexte, comme à une des coordonnées de la mesure. Ainsi, dans la question : « Approuvez-vous ou non la diffusion des OGM dans l'agriculture ? », l'expression « dans l'agriculture » précise la signification des OGM pour les sujets interrogés.
- 9/ Éviter les propositions qui pourraient être adoptées par tout le monde.
- 10/ Évaluer, autant que possible, la confiance que chaque personne met dans la réponse qu'elle donne à une question.
Pourquoi formulons-nous justement ces règles ? Eh bien, à leur source, on peut considérer les échelles comme un moyen de recherche d'informations et d'observations plus ou moins fines. Mais elles commencent à exister seulement à partir du moment où elles sont conçues en vue de la mesure. Et celle-ci présuppose certaines règles de construction, de lecture et de calcul. Quand on veut utiliser un thermomètre, on conçoit toutes ses propriétés avant de le plonger dans un liquide chaud ou froid. Ce n'est pas n'importe quel tube plongé dans un tel liquide qu'on baptise thermomètre après l'en avoir retiré parce qu'il indique un certain chiffre. Et pourtant, c'est bien ainsi que certains procèdent avec les échelles. Ils commencent par établir un questionnaire sur un sujet donné - la santé, le tabagisme, etc. - et après l'avoir appliqué à une population, ils essaient de voir s'il forme ou non une échelle. Au contraire, celle-ci doit être conçue d'emblée de manière hypothétique et le questionnaire par exemple ordonné et formulé de façon à la mettre en évidence. Les règles énumérées visent à en faire un bon instrument [318] de mesure. Il faut les respecter d'autant plus scrupuleusement que les possibilités de mesure dans les sciences de l'homme sont limitées, voire modestes. La raison pratique en est la forte interaction entre l'observateur et les phénomènes observés. Et la raison théorique, c'est l'absence d'une métrique ou de constantes universelles qui permettraient d'évaluer le degré de précision des mesures. Si, en dépit de toutes ces difficultés, on obtient des résultats, c'est admirable. Et sans doute aucune échelle ne vient-elle au jour aussi rigoureuse et aussi achevée que dans la vision de son concepteur.
2. Échelles nominales et échelles ordinales
- 2.1. Échelles nominales

Il s'agit de la manière la plus élémentaire de mesurer les choses : on les nomme. En nommant différemment, on établit des différences et les objets sont affectés à des classes différentes.
Une entreprise peut définir des régions commerciales (par ex. : Sud, Nord, Est, Ouest) et donc, chacun de ses clients appartiendra à une de ces régions commerciales (une classe).
TABLEAU 1. — Membre de clients par régions commerciales
|
Régions commerciales
|
Effectifs
|
|
Sud
|
1 510
|
|
Nord
|
2 200
|
|
Est
|
1 250
|
|
Ouest
|
1 820
|
|
Total
|
6 780
|
Les variables nominales sont des variables discrètes, c'est-à-dire qu'elles ne sont pas représentables sur un continuum, elles constituent seulement des classes disjointes. Elles marquent la différence entre individus de deux classes différentes et la similitude entre individus d'une même classe.
La qualité d'une échelle nominale dépend de sa capacité à affecter chaque individu d'une population à une catégorie et une seule et à affecter tous les individus de la population. Il faut donc que les classes ne se chevauchent pas [1].
[319]
- 2.1.1. Propriétés des échelles nominales
La représentation graphique classique de ce type d'échelle est l'histogramme. On représente, côte à côte les différentes classes, et, pour chacune d'elle, une barre verticale indique le nombre d'individus qu'elle contient.
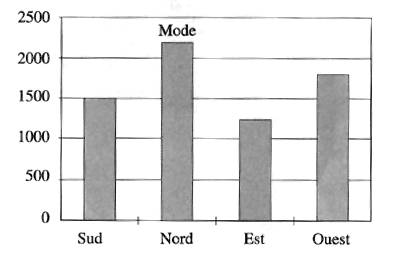
SCHÉMA 1. — Répartition des clients en fonction des régions
On peut désigner le mode de la distribution, c'est la classe qui a le plus d'individus. On peut calculer des fréquences, c'est-à-dire la probabilité qu'un individu appartienne à une classe.
TABLEAU 2. —
Effectifs et pourcentage de clients par régions commerciales
|
Régions commerciales
|
|
|
|
Sud
|
|
|
|
Nord
|
|
|
|
Est
|
|
|
|
Ouest
|
|
|
|
Total
|
|
|
On peut aussi calculer l'entropie. L'entropie, c'est la capacité à prédire l'appartenance d'un individu à une classe. Elle est d'autant plus faible qu'il y a beaucoup de classes et elle est également d'autant plus faible que la répartition des effectifs entre les classes est homogène (s'il n'y a que 2 classes, la prédiction est plus aisée que s'il y a 100 classes ; si une seule classe contient 90% des individus, la prédiction est plus aisée que si toutes les classes contiennent le même pourcentage d'individus).
[320]
La représentation graphique typique de ces fréquences est le camembert. Il représente les différentes classes et révèle la proportion d'individus que chaque classe contient.

SCHÉMA 2. — Répartition des clients en fonction des régions
Si un même ensemble d'individus est classé en fonction de deux critères qui sont tous deux des échelles nominales, on peut étudier l'indépendance de ces deux échelles ou critères : c'est le test de Chi2. On vérifie si la répartition observée s'écarte significativement de la répartition théorique. Si tel est le cas, on rejette l'hypothèse d'indépendance.
- 2.2. Échelles ordinales

Une échelle ordinale a les mêmes exigences que l'échelle nominale :
- un individu doit être affecté à une classe et une seule ;
- les classes ne doivent pas se superposer et doivent être ordonnées.
Il faut donc établir une relation d'équivalence entre les individus et un certain nombre de classes disjointes mais en plus, il faut ordonner les classes.
TABLEAU 3. — Niveau d'étude du personnel de l'entreprise ET & CO
|
Diplôme
|
Inférieur
à CE
|
CE
|
BEPC
|
BAC
|
DEUG
|
2e cycle
universitaire
|
3e cycle
universitaire
|
Total
|
|
Effectifs
|
14
|
5
|
19
|
36
|
22
|
27
|
9
|
132
|
|
%
|
11
|
4
|
14
|
27
|
17
|
20
|
7
|
100
|
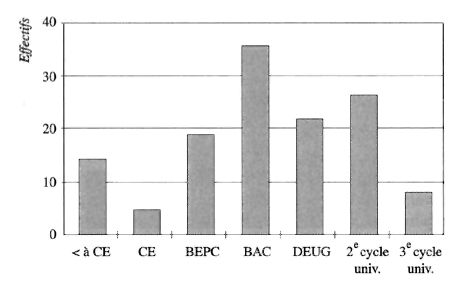
SCHÉMA 3. — Niveau d'étude du personnel
de l'entreprise ET & CO (effectifs)
- 2.2.1. Propriétés des échelles ordinales
Les échelles ordinales possèdent les propriétés des échelles nominales, mais le fait d'ordonner les classes leur confère des propriétés supplémentaires, notamment la transitivité (si A ≥ S et B ≥ C, alors A ≥ C).
On peut calculer la médiane. C'est la classe à partir de laquelle plus de 50% des individus ont été classés (et ordonnés).
On peut calculer le centile, le décile... C'est la classe à partir de laquelle plus de x% des individus ont été classés (et ordonnés) ; on parle de 1er centile ; de 2e centile...
Ainsi, considérant que l'individu qui a un 3e cycle universitaire a aussi un 2e cycle universitaire et un 1er cycle universitaire et le BAC et le BEPC et le CE et les niveaux inférieurs au CE, on peut le compter dans chacune de ces catégories. Si l'on fait de même pour chaque individu, on obtient des effectifs cumulés.
TABLEAU 4. —
Niveau d'étude du personnel de l'entreprise ET & CO (effectifs cumulés)
|
Diplôme
|
Inférieur
à CE
|
CE
|
BEPC
|
BAC
|
DEUG
|
2e cycle
universitaire
|
3e cycle
universitaire
|
|
Effectifs cumulés
|
132
|
118
|
113
|
94
|
58
|
36
|
9
|
|
% cumulés
|
100
|
89
|
86
|
71
|
44
|
27
|
7
|
Par exemple, dans la catégorie BAC en effectif cumulé on obtient 94. Ces 94 sont la somme de ceux qui n'ont que le BAC (36) + ceux qui ont aussi un DEUG (22) + ceux qui ont aussi un 2e cycle universitaire (27) + ceux qui ont un 3e cycle universitaire (9). Tous ces individus ont bien au moins le bac.
[322]
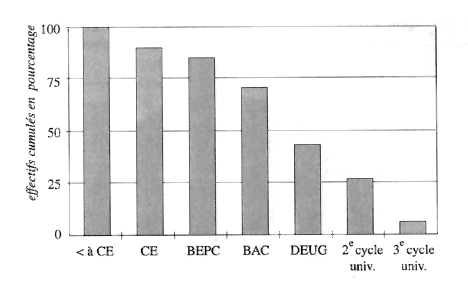
SCHÉMA 4. — Niveau d'étude du personnel de l'entreprise ET & CO
(effectifs cumulés en %)
Sur le schéma 4, on voit apparaître les quartiles (1er quartile ; classe à partir de laquelle 25% des individus ont été classés ; 3e quartile : classe à partir de laquelle 75% des individus ont été classés) et la médiane ou 2e quartile (classe à partir de laquelle 50% des individus ont été classés).
Si un même ensemble de données est classé en fonction de 2 critères qui sont tous deux des échelles ordinales, on peut étudier l'indépendance de ces deux échelles ou critères : c'est le coefficient de corrélation par rang de Kendall. On vérifie si la répartition observée s'écarte significativement de la répartition théorique. Si tel est le cas, on rejette l'hypothèse d'indépendance. On peut aussi utiliser un coefficient par rangs de Spearman (c'est-à-dire un coefficient de Bravais-Pearson calculé sur les rangs et non sur les données brutes).
3. Les échelles de distance sociale

L'échelle de Bogardus est la première du genre. Née en 1923, elle est destinée à mesurer la distance sociale (Bogardus, 1925), c'est-à-dire la distance qui sépare un groupe d'un autre groupe. Elle fut donc destinée à mesurer les rapports de discrimination entre groupes ethniques, nationaux, religieux (Bogardus, 1933).
L'échelle se compose d'une série d'énoncés portant sur des situations imaginaires, mais néanmoins issues de la vie courante : manger avec un X, se marier avec un X, habiter la même ville que des X, aller à la même école que des X ... X étant des Noirs, des Japonais, des Chinois, des Italiens, des Catholiques, des Mormons...
L'échelle se fonde sur la proximité plus ou moins grande de ces X au sujet dans diverses situations. La plus petite proximité acceptable est censée indiquer l'attitude de l'individu vis-à-vis du groupe en question :
[323]
- - j'accepte mut à fait qu'il y ait des Chinois dans mon pays :
- - j'accepte tout à fait qu'il y ait des Chinois dans mon département ;
- - j'accepte tout à fait qu'il y ait des Chinois dans ma ville ou mon village ;
- - j'accepte tout à fait d'avoir des Chinois comme voisins ;
- - j'accepte tout à fait d'avoir des Chinois comme amis ;
- - j'accepte tout à fait que ma fille épouse un Chinois.
On voit que le fait d'accepter l'un de ces énoncés implique généralement que l'on accepte aussi les énoncés qui le précédent. Il suffit donc de connaître le dernier énoncé accepté, celui qui marque la distance minimale acceptée pour connaître l'attitude de l'individu vis-à-vis du groupe en question. Cette échelle peut être adaptée aux cas étudiés. La distance étudiée est certes une distance sociale, mais son expression en termes de distance physique est judicieuse. Dans certains cas, on pourra proposer des énoncés portant sur l'acceptation de serrer la main, de manger avec...
Avec cette échelle, on lit directement l'attitude de l'individu et on connaît aussi sa place par rapport aux attitudes d'autres individus.
Cette échelle peut permettre de comparer l'attitude vis-à-vis de différents groupes en proposant aux sujets un questionnaire bâti de la manière suivante.
TABLEAU 5. — Échelle de distance sociale pour différents groupes
|
J'accepte tout à fait les
|
Allemands
|
Autrichiens
|
Anglais
|
Suisses
|
Italiens
|
Portugais
|
Polonais
|
Russes
|
Turcs
|
…
|
…
|
…
|
Comme:
|
|
touristes
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- habitants de mon pays
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- voisins
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- amis
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- proches parents
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Mettez un «O» pour «Oui» dans les cases où vous acceptez.
Mettez un «N» pour «Non» dans les cases où vous refusez.
|
D'après la description des échelles, il est clair que l'on ne prête aucune attention au problème de la mesure en tant que tel. Il suffit que les énoncés relatifs à un objet social donné puissent être classés de manière à signifier soit une proximité, soit un éloignement. Les échelles construites de cette façon donnent des résultats à la fois intéressants et valides.
[324]
4. Les Échelles de Thurstone
pour la mesure des attitudes

La psychologie sociale est initialement une science des attitudes. Ce n'est pas notre rôle, ni notre propos, d'exposer et de discuter concrètement la notion ou l'évolution de la discipline qui a réduit la notion et réduit son importance (Moscovici, 1963). La mesure des attitudes, c'est autre chose. Elle a trait à quelques principes et à toute une série de techniques qui permettent de mettre en rapport des réponses à un questionnaire et de classer les sujets qui y répondent. En un sens, elles calquent la démarche de Fechner et Weber qui s'applique aux stimuli psychophysiques, à la possibilité d'établir une échelle d'intensité des réponses, des sensations, à celle des stimuli lumineux, tactiles, et ainsi de suite. Ces contributions à la difficile et séduisante question des lois psychophysiques ont été à l'origine des tentatives analogues faites en psychologie sociale, sinon dans l'esprit qui était romantique, du moins dans leurs applications concrètes. Vers les années 1920, Thurstone a publié une série d'articles dans lesquels il a explicité sa loi du jugement comparatif. Cette prétendue loi fut significative, parce qu'elle fournissait une analyse raisonnée permettant d'ordonner les stimuli selon un continuum psychologique comportant toutes les sortes de valeurs et d'expériences subjectives. C'est-à-dire de construire des échelles en supposant que, étant donné n'importe quel ensemble donné de n stimuli, des opinions et des jugements inclus, nous pouvons supposer que chacun d'eux possède à un degré variable quelque attribut qui nous intéresse. Le problème de cet échelonnage psychologique ou social consiste alors à déterminer si les n stimuli peuvent être ordonnés selon un continuum, sur une dimension, selon le degré de cet attribut qu'ils possèdent. Les techniques d'échelonnage psychologique ne garantissent cependant pas que le résultat final sera une réussite, c'est-à-dire que l'on trouvera un continuum psychologique pour chacun des attributs pris un à un. Cela dépend à la fois de l'analyse théorique préalable du phénomène étudié et de sa mise en œuvre par le questionnaire établi.
Tout cela, bien entendu, complique ce qui était assez simple dans les échelles nominales et ordinales. Avec celle-là, on nous demandait simplement de distinguer et de compter. Ici, on nous demande de mesurer et de mesurer à partir de valeurs et de jugements qui présupposent une tendance, un principe ou une dimension que chaque valeur ou jugement manifeste. Les conditions d'établissement d'une telle échelle sont précises, si l'on veut que ses mesures soient exactes. On désire que tout parti pris, toute incertitude soient bannis, et donc on constitue d'abord un groupe de juges qui doivent catégoriser de la manière la plus impersonnelle les énoncés proposés par les chercheurs. C'est seulement ensuite que d'autres individus ou des sujets se prononcent sur les énoncés retenus par les juges. Ceci présuppose qu'il y ait une distanciation et que les attitudes propositionnelles, les questions, changent de niveau, qu'elles aient un sens plus abstrait, plus commun et général. Cette exigence apparaîtra mieux si l'on considère plusieurs méthodes de construction des échelles elles-mêmes.
[325]
- 4.1. La méthode de comparaison par paires

Dans une première version de la méthode, la méthode de comparaison par paires, les sujets-juges doivent juger des énoncés pris deux à deux et décider quel énoncé est le plus favorable et lequel est le plus défavorable (Thurstone, 1929 b).
Prenons par exemple les 3 énoncés suivants :
- - énoncé A : Je suis croyant, bien que faille rarement à l'église ;
- - énoncé B : J'aime beaucoup la musique des cérémonies religieuses ;
- - énoncé C : Ce qui se passe à l'église n'est qu'hypocrisie et préjugé.
En comparant les paires d'énoncés (A, B), (B, C) et (A, C), les sujets-juges (N = 30) choisis vont faire les estimations suivantes :
- - l'énoncé A est plus favorable que l'énoncé B : 21 « Oui » et 9 « Non » ;
- - l'énoncé A est plus favorable que l'énoncé C : 29 « Oui » et 1 « Non » ;
- - l'énoncé B est plus favorable que l'énoncé C : 25 « Oui » et 5 « Non ».
On voit donc que l'énoncé A est jugé plus favorable que l'énoncé B et que l'énoncé C (A > B et A > C) et que l'énoncé B est jugé plus favorable que l'énoncé C {B > C).
On peut supposer que ces énoncés se classent suivant cet ordre : A > B > C.
En plus du simple classement, on peut évaluer les distances séparant ces énoncés en observant la répartition des sujets-juges entre le « Oui » et le « Non » pour chaque comparaison de paires. S'il y a autant de « Oui » (50%) que de « Non » (50%), les deux énoncés sont exactement aussi favorables l'un que l'autre (ils seront au même endroit sur l'échelle) et plus la proportion s'écarte de cette égalité, plus les deux énoncés sont différents l'un de l'autre (ils seront donc plus distants sur l'échelle).
En fait, il y a trois jugements possibles en ce qui concerne une comparaison par paires : « A < B » ; « A > B » et « A = B » et chaque sujet-juge va retenir l'un de ces jugements. On doit admettre que si en réalité A est supérieur à B, alors le dépouillement des résultats relatifs aux choix des sujets-juges donnera un nombre majoritaire de sujets-juges choisissant le jugement « A > B » et un nombre moindre de juges choisissant un autre jugement. Objectivement, du point de vue de la réalité, il y a des jugements justes et des jugements faux. Ces jugements justes et ces jugements faux sont d'autant plus facilement discernables que les objets ou énoncés sur lesquels ils portent sont objectivement différents. Par exemple, il y une différence objective entre un poids de 500 g et un poids de 900 g tout comme il y a aussi une différence objective entre un poids de 500 g et un poids de 505 g, mais cette seconde différence est beaucoup moins facilement discernable que la première.
Ainsi, la proportion de jugements « A > B » qui sera donnée par les juges est un indice de distance entre les énoncés A et B :
- la distance est minimale lorsque 50% des sujets-juges pensent que « A > B » et que 50% pensent au contraire que « A < B » ;
- la distance est maximale lorsque 100% des sujets-juges pensent que « A > B » (et 0% que « A < B ») ou lorsque 100% pensent que « A < B » (et 0% que « A > B »).
[326]
On voit donc que, plus la répartition s'écarte de l'équi-répartition, plus les deux objets ou énoncés sont distants l'un de l'autre. La distance entre deux énoncés peut nous être donnée plus précisément si l'on suppose que l'attitude et ses niveaux sont proches de la loi normale.
Pratiquement, à l'issue du dépouillement des décisions des juges, pour chaque paire, on connaît la probabilité qu'un énoncé soit considéré comme plus favorable qu'un autre énoncé. Si Ton suppose que la distribution de ces jugements comparatifs est normale, alors avec ces deux informations on peut trouver une distance entre les deux énoncés.
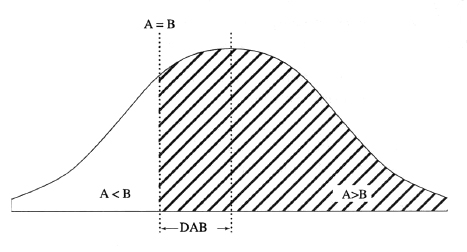
SCHÉMA 5. — Distribution des probabilités de choix (loi normale)
Nous savons que l'énoncé A est plus favorable que l'énoncé B pour 21 juges sur 30, donc dans 70% des cas (ce 70% est représenté sur le graphique par la surface hachurée et les 30% par la surface non hachurée). L'intégrale (la surface hachurée) est donc égale à 0,7, ce qui permet de trouver l'abscisse correspondante (axe où la verticale « A = B » coupe l'abscisse) sur une table de loi normale : pour Iab = 0,7 on obtient Dab = 0,525 (cette distance est nommée le z-score) [2].
Techniquement voici comment on construit l'échelle avec nos trois énoncés.
Pour chaque paire d'énoncés, on a la probabilité que l'un soit jugé plus favorable que l'autre. On peut donc établir le tableau des probabilités, le tableau 6.
[327]
TABLEAU 6. — Probabilité que l'énoncé indiqué en colonne
soit jugé plus favorable que l'énoncé indiqué en ligne 1
|
|
Énoncé A
|
Énoncé B
|
Énoncé C
|
|
Énoncé A
|
|
0,70
|
0,97
|
|
Énoncé B
|
0,30
|
|
0,83
|
|
Énoncé C
|
0,03
|
0,17
|
|
|
l. Probabilité (A > B) + Probabilité (B > A) = 1.
|
À partir de ces probabilités, on calcule le tableau des z-scores correspondants.
TABLEAU 7. z-scores des probabilités que l'énoncé indiqué en colonne
soit jugé plus favorable que l'énoncé indiqué en ligne 1
|
|
Énoncé A
|
Énoncé B
|
Énoncé C
|
Moyenne
|
|
Énoncé A
|
0
|
0,525
|
+1,882
|
0,802
|
|
Énoncé B
|
-0,525
|
0
|
0,965
|
0,147
|
|
Énoncé C
|
-01,882
|
-0,965
|
0
|
-0,949
|
|
1. z-score (A > B) + z-score (B > A) = 0.
|
En calculant la moyenne, pour chaque énoncé, des z-scores, on obtient la place de cet énoncé sur une échelle unidimensionnelle.

SCHÉMA 6. — Échelles d'attitude vis-à-vis de l'église
(bâtie sur seulement 3 énoncés)
L'échelle ainsi obtenue peut être vérifiée. Il suffit, à partir de la valeur de l'échelle, d'obtenir des prédictions sur les choix des individus à propos des comparaisons par paires des énoncés. En définitive, on fait le chemin inverse de la construction d'échelle : à partir des valeurs des énoncés sur l'échelle, on reconstitue les probabilités, donc les prédictions des comparaisons par paires. Il suffira, ensuite de comparer ces prédictions aux choix réels des individus.
[328]
TABLEAU 8. — Établissement de la probabilité
à partir de la distance sur l'échelle
|
|
Distance sur l'échelle
|
Probabilité prédite
|
Probabilité observée
|
Différence
|
|
Dab
|
0,655
|
0,744
|
0,70
|
0,044
|
|
DAC
|
1,751
|
0,960
|
0,97
|
0,01
|
|
Dbc
|
1,096
|
0,863
|
0,83
|
0,03
|
Par exemple, la valeur de l'énoncé A sur l'échelle est de + 0,802, celle de B est de + 0,147. Es sont donc distants de 0,655. Or, cette distance (z-score) correspond à la probabilité suivante : 0,744. Ainsi, à partir des valeurs de l'échelle on prédit que 74,4% individus vont juger que l'énoncé A est plus favorable que l'énoncé B. Le résultat observé est de 70% (21 individus sur 30) et le résultat prédit est de 74,4%.
TABLEAU 9. — Comparaison des répartitions de choix observés et prédits
|
L'énoncé A est plus favorable
que l'énoncé B
|
Choix observés
|
Choix prédits
|
|
Oui
|
70% (21 juges)
|
74,4%
|
|
Non
|
30% (9 juges)
|
25,6%
|
Ces différences de proportions peuvent être comparées par un test de Chi2 afin de savoir si elles différent significativement l'une de l'autre. Si elles ne différent pas, significativement, l'échelle représente bien les choix des individus.
Ce type de constitution d'une échelle a l'avantage de reposer sur des jugements que les individus peuvent faire aisément : ils sont tout à fait capables de dire si deux énoncés sont ou non égaux. Le principal problème de cette méthode est le nombre d'énoncés à comparer deux à deux, donc le nombre de paires. Ce nombre se calcule avec la formule suivante :  (n étant le nombre d'énoncés). Par exemple, avec 20 énoncés, il y a 190 paires à évaluer. (n étant le nombre d'énoncés). Par exemple, avec 20 énoncés, il y a 190 paires à évaluer.
- 4.2. La méthode des intervalles a priori égaux

C'est notamment afin de simplifier la méthode des comparaisons par paires que cette méthode a été élaborée.
On place devant chaque sujet-juge une série de cartons marqués de I à XI, on les ordonne devant lui par ordre croissant et on lui explique que ces cartons marquent les étapes du « tout à fait favorable » au « tout à fait défavorable » à l'église, pour reprendre le même thème que précédemment. On établit ainsi un continuum unidimensionnel.
[329]
Ensuite, on fournit au sujet-juge une pile de petits papiers. Sur chaque petit papier, il y a un énoncé et le sujet-juge doit placer ce papier sur le carton ou la catégorie qui lui semble approprié. Ainsi, plus l'énoncé se retrouve sur un carton proche dé I, à gauche, et plus il est favorable à l'église, tandis que plus il se trouve vers le carton XI, à droite, et plus il est défavorable à l'église. Un énoncé, ni favorable ni défavorable, se retrouve proche du carton VI ou même sur ce carton qui marque le centre.
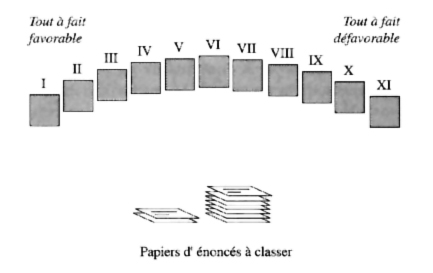
SCHÉMA 7. — Procédure et matériel pour le classement des énoncés
Ainsi, à la fin, lorsque tous les sujets-juges ont effectué la répartition des énoncés dans les différentes catégories, on peut calculer, pour chaque énoncé, sa probabilité d'être dans telle ou telle catégorie.
Cependant, il n'est pas toujours possible de jalonner régulièrement l'ensemble du continuum (Lemaine, 1972). Parfois, la plupart des énoncés se situent sur une partie de l'échelle laissant d'autres parties vides.
TABLEAU 10. — Exemple de répartition d'énoncés (A, B, C, D)
par des sujets-juges en fonction des 11 catégories (de I à XI) (en%)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Énoncé A
|
|
|
|
|
|
|
|
|
|
|
|
|
Enoncé B
|
|
|
|
|
|
|
|
|
|
|
|
|
Enoncé C
|
|
|
|
|
|
|
|
|
|
|
|
|
Enoncé D
|
|
|
|
|
|
|
|
|
|
|
|
- Énoncé A : Les gens qui sont pratiquants sont tristes.
- Énoncé B : J'assiste assez régulièrement à des cérémonies religieuses.
- Énoncé C : Le message de l'église devrait être un peu actualisé.
- Énoncé D : L'église exerce une fonction sociale.
[330]
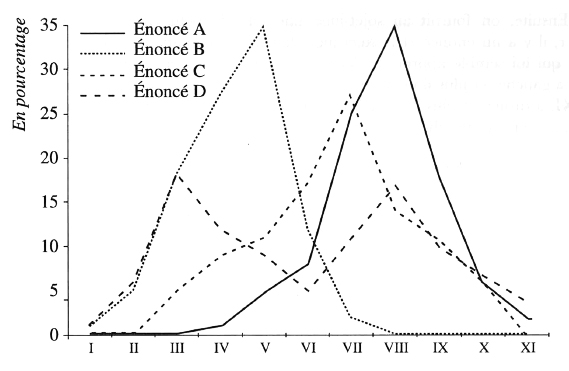
SCHÉMA 8. — Graphique de la répartition des énoncés
Chaque énoncé peut être défini par sa valeur moyenne et sa dispersion.
Certains énoncés se distribuent approximativement suivant une loi normale et se trouvent bien marqués par une catégorie, c'est le cas des énoncés A, B et C.
Par contre d'autres énoncés, comme l'énoncé D, peuvent avoir une distribution bi-modale, ce qui oblige à les éliminer pour ne conserver que ceux qui sont bien représentés par une seule catégorie. On peut aussi éliminer les énoncés dont la dispersion est très élevée.
Pour connaître le score de chaque énoncé, on peut postuler que les écarts entre catégories sont égaux et on affectera un coefficient à chaque catégorie (1=1 ; 11=2... XI = 11).
En pondérant ces valeurs par les effectifs, on peut trouver le score de chaque énoncé. Le calcul se fait de la manière suivante pour l'énoncé A :
0x1 + 0x2 + 0x3 + 1x4+5x5 + 8x6+25 x7
|
+ 35x8 + 18x9 + 6x10 + 2x11
|
= 7,76.
|
|
0 + 0 + 0 + 1 + 5 + 8 + 25 + 35 + 18 + 6+2
|
On obtient ainsi 7,76 pour A, 4,34- pour B et 6,68 pour C.
Ces trois énoncés constituent donc 3 échelons différents d'une échelle dont le minimum est 1 et le maximum 11. Pour bien différencier les individus, il faut, bien sûr, d'autres échelons.
Pour connaître la valeur de l'attitude d'un individu répondant à une échelle de Thurstone, il suffit de faire la moyenne des scores des énoncés qu'il a acceptés. Si, par exemple, il a seulement accepté l'énoncé B et l'énoncé C, son attitude a la valeur suivante : (4,34 + 6,68)72 = 5,51. Un individu ayant accepté les trois énoncés (A, B et C) [331] aura une attitude dont la valeur est la suivante : 4,34 + 6.68 - 7.76)/3 = 6.26. Un individu n'acceptant que l'énoncé A ayant une attitude de valeur égale à 7,76.
Avoir une attitude très favorable à l'objet, ce n'est donc pas accepter beaucoup d'énoncés, mais c'est accepter ceux qui ont le score le plus fort. Cette idée est assez juste, puisque les sujets les plus impliqués ont une latitude de rejet (non-choix des énoncés s'écartant de leur position) beaucoup plus étendue et une latitude d'acceptation beaucoup plus réduite que les sujets moins impliqués ou ayant des positions plus centrales.
Le grand changement que ces échelles ont introduit en psychologie sociale est, semblerait-il, un changement de vision, donc de style. Le chercheur n'est plus soumis aux aléas de la diversité des valeurs et des jugements ponctuels. Il n'est plus débordé par la masse des données et des chiffres. Il n'est pas réduit au discours rhétorique et ne justifie plus au lieu d'analyser quand il décrit sa recherche. Il acquiert la capacité de se concentrer sur la conception d'un ordre de phénomènes, d'une classification des individus, sans se laisser distraire par des détails incertains. Sans doute y a-t-il une difficulté de lecture de ces échelles, jointe à la tentative de les mettre en rapport entre elles. Mais c'est le prix à payer, car les chercheurs obéissent encore à un autre ordre, celui que leur impose la convention scientifique. Et comme ils ne sont pas les arbitres de cette convention et que la science est en grande partie basée sur des mesures et des quantifications, celles-ci ont ainsi la prééminence.
Toutefois il est probable que, dans la science comme dans la vie, on constate sans cesse que les conventions que l'on adopte par nécessité ou déférence envers l'autorité n'ont pas la fermeté qu'on leur attribue. On le pensait par avance, encore faut-il le prouver. Pour commencer, il y a cette difficulté psychique, sociale, simple en apparence, en réalité si gênante, d'être objectif sur des questions importantes, de prendre une distance par rapport aux valeurs, d'être juge ou membre d'un jury sans tenir compte de ses préférences ou d'un climat d'opinion. Et pourtant c'est la condition même, donc essentielle, de la construction de ces échelles. Pour cette raison, des études ont été faites concernant la relation entre les valeurs des échelles d'énoncés et l'attitude des juges opérant le tri. Dans l'une d'elles, Hinkley (1932) a fait appel à trois groupes de juges qui pourraient avoir des attitudes différentes envers les Noirs. L'un est un groupe de sujets blancs du Sud qui pourraient avoir une attitude défavorable aux Noirs. Un autre groupe se compose de Blancs du Nord, censés avoir une attitude favorable envers les Noirs, et le troisième groupe est constitué de Noirs. Chaque groupe de sujets est chargé de distribuer plus d'une centaine d'énoncés entre 11 catégories suivant la procédure des intervalles a priori égaux. Hinkley a trouvé que les énoncés étaient ordonnés de la même façon sur le continuum psychologique, et en a conclu que les valeurs des échelles d'énoncés étaient indépendantes des groupes qui les jugeaient.
Mais il reste vrai que, si certaines études ont confirmé ces résultats, d'autres ont semblé montrer, au contraire, que le jugement de ces juges dépendait de leurs attitudes préalables. Elles ne furent pourtant pas assez convaincantes, de sorte qu'on resta longtemps persuadé que toutes les tentatives pour réfuter l'hypothèse que les valeurs des échelles d'énoncés sont indépendantes de l'attitude de ceux qui les trient étaient vouées à l'échec. Certes, les chercheurs devaient avoir leur propre façon d'opérer pour ne pas [332] voir ce que le fait avait d'étrange et même d'invraisemblable. En 1952, les temps ayant changé, Hovland et Shérif affirment que l'on dispose de preuves insuffisantes de ce que les groupes de juges, censés différer par leurs attitudes, en fait incluent des individus qui se situent aux extrémités opposées du continuum. Ils avancent l'hypothèse que les juges qui ont une attitude extrêmement favorable ou extrêmement défavorable devraient restreindre à un très petit nombre les catégories dans lesquelles ils placent les énoncés. Ils émettent une seconde hypothèse : les juges ayant une attitude extrême devraient faire preuve d'une grande discrimination dans les énoncés qu'ils placent vers leur propre extrémité de l'échelle et faire preuve d'une tendance symétrique en groupant les énoncés à l'extrémité opposée de l'échelle. En utilisant la même procédure que Hinkley, ils ont prouvé ces hypothèses de manière satisfaisante (Hovland et Shérif, 1952 ; Shérif et Hovland, 1953).
De toute évidence, il est impossible de trouver les mêmes résultats dans toutes les expériences, ou en utilisant toutes les méthodes. Quoi qu'il en soit, on ne croit pas à la nécessité de ces juges, à leur distance supposée pour construire ces échelles. À en juger par la pratique, les principes statistiques et les calculs suffisent à former une échelle en partant des réponses de la population elle-même.
5. L'échelle de Lickert

En 1932, Lickert met au point une méthode plus simple que celles de Thurstone. D réalise une étude portant sur trois thèmes : l'impérialisme, l'internationalisme et les Noirs. Son questionnaire nécessite donc la construction de trois échelles.
Pratiquement, il propose des batteries d'énoncés que les sujets doivent évaluer. Ces énoncés et leur mode d'évaluation sont choisis pour leur capacité discriminante, il faut que deux individus ayant une attitude différente ne se positionnent pas de la même manière. Ainsi, les énoncés d'une échelle de Lickert ne portent pas sur des faits et ils sont souvent rédigés au conditionnel (ex. : « Si le même travail de préparation est nécessaire, l'instituteur noir devrait recevoir le même salaire que son collègue blanc » ; « Les États-Unis devraient consulter les autres nations avant de faire des lois sur l'immigration »). De plus, pour évaluer chaque énoncé, les sujets disposent de plusieurs modalités de réponses et chacune de ces modalités de réponse est codée par une note dont la valeur varie en fonction de l'évaluation qui est faite du thème.
TABLEAU 11. — Exemples d'énoncés à propos de l'impérialisme
« Si un Américain traite des affaires en Chine, il doit accepter de se soumettre aux lois chinoises. »
|
Approbation
totale
|
Approbation
|
Indécision
|
Désapprobation
|
Désapprobation
totale
|
|
(5)
|
(4)
|
(3)
|
(2)
|
(1)
|
[333]
« Nous devrions intervenir militairement chaque fois que nos investissements en Amérique du Sud sont menacés. »
|
Approbation
totale
|
Approbation
|
Indécision
|
Désapprobation
|
Désapprobation
totale
|
|
(1)
|
(2)
|
(3)
|
(4)
|
(5)
|
Comme on le voit dans ces deux exemples, plus la note est faible, plus les sujets se positionnent comme des impérialistes.
En additionnant les notes obtenues par un sujet à chaque énoncé concernant l'impérialisme, on obtient un score révélateur de son attitude vis-à-vis de l'impérialisme.
S'il y a 12 questions codées de 1 à 5, les scores peuvent aller de 12 (12 * 1) à 60 (12 * 5). Dans ce cas, il y a donc 49 niveaux sur lesquels on peut classer les attitudes des sujets.
Pour chaque énoncé, on peut calculer sa corrélation avec le score à l'échelle. Plus cette valeur est élevée (max = + 1), plus l'énoncé contribue à la construction du score. Une note négative indique que le codage doit être inversé ou que la question n'a pas été bien comprise des sujets.
En plus d'une matrice de corrélation, on peut utiliser des tests de concordance entre énoncés. L'un des plus utilisés est l'alpha de Cronbach. Ce test indique l'alpha pour les énoncés sélectionnés. On considère habituellement qu'au-dessus de 0,6 l'échelle est acceptable et qu'au-dessus de 0,8 elle est très bien. Ce test indique aussi les valeurs que prendrait l'alpha de Cronbach si l'on enlevait de l'échelle chacun des énoncés pris un à un. Ceci permet éventuellement d'affiner l'échelle.
6. La méthode de dépliage

Les échelles de Thurstone reposent notamment sur l'idée qu'une fois que les énoncés de l'échelle ont été classés du plus favorable au moins favorable vis-à-vis de l'objet étudié, tous les individus de la population sont d'accord avec ce classement. C'est une supposition dont la méthode de dépliage proposée par Coombs (1950, 1964) n'a pas besoin.
Prenons les quatre énoncés suivants à propos de la politique de discrimination positive vis-à-vis des individus issus de groupes minoritaires.
- - Énoncé A : Dans les écoles supérieures, il est nécessaire de réserver au moins 10% des places pour les individus provenant de groupes minoritaires.
- - Énoncé B : Dans le système éducatif, il est nécessaire de mettre en place des cours de soutien spécialement adaptés aux individus provenant de groupes minoritaires.
- - Énoncé C : Il faut favoriser les individus provenant de groupes minoritaires, mais on ne doit pas défavoriser les autres.
- - Énoncé D : Seul le mérite compte, il est intolérable défavoriser certains individus sur la base de critères d'origine sociale, nationale, religieuse...
[334]
Chaque énoncé est plus ou moins favorable à la politique de discrimination positive. Le plus favorable est le A, puis le B, puis le C et enfin, le moins favorable est le D. Le classement est donc : A > B > C > D.
Mais que vaut ce classement ? Est-il valable pour tous les individus comme le suppose l'échelle de Thurstone et en outre, est-il intéressant pour saisir l'attitude des individus ?
Si l'on prend un individu extrêmement favorable (ÏEXT+) à la politique de discrimination positive, il choisira d'abord l'énoncé A qui sera l'énoncé le plus proche de sa position. Ensuite, il sera plus proche de l'énoncé B que du G, puis plus proche de l'énoncé C que de l'énoncé D.
Si l'on prend maintenant un individu extrêmement défavorable (Iext-) à la politique de discrimination positive, il choisira d'abord l'énoncé D qui sera l'énoncé le plus proche de sa position. Ensuite, il sera plus proche de l'énoncé C que du B, puis plus proche de l'énoncé B que de l'énoncé A.
Ainsi, pour ces extrémistes, les positions ou les points de vue changent, mais l'ordre des énoncés reste contant.
Voyons maintenant le cas des autres individus, ceux qui ont une position intermédiaire.
Un individu favorable mais seulement assez modérément favorable (Ifav) à la politique de discrimination positive, se situera, sur cette échelle, vers l'énoncé B qui sera l'énoncé le plus proche de sa position. Ensuite, cet individu choisira peut-être l'énoncé A puis le G et enfin le D.
Un individu défavorable mais seulement assez modérément défavorable (ÏDEF) à la politique de discrimination positive, se situera, sur cette échelle, vers l'énoncé C qui sera l'énoncé le plus proche de sa position. Ensuite, cet individu choisira peut-être l'énoncé D puis le B et enfin le A.
Sur la base de ces préférences individuelles, on obtient pour chaque individu un classement qui lui est propre : c'est l'échelle individuelle (« i scale ») qui possède un point idéal, c'est-à-dire la position que l'individu préfère, et un classement des autres énoncés par ordre décroissant de préférence.
- - pour l'individu IEXT+, sa préférence est A et le classement :
A > B > C > D ;
- - pour l'individu Iext-, sa préférence est D et le classement :
D > C > B > A ;
- - pour l'individu Ifav, sa préférence est B et le classement :
B > A > C > D ;
- - pour l'individu Idef, sa préférence est C et le classement :
C > D > B > A.
Il y a autant d'« i scale » que d'individus. Tout le problème de la méthode de Coombs est de représenter ces diverses « i scale » sur une seule et même échelle (« j scale »). Compte tenu de ces choix individuels peut-on élaborer une échelle sur laquelle, par dépliage, seront représentés correctement les choix des individus ?
Enfin, notons que d'après Coombs lorsqu'on demande un tel classement à un individu, il fournit une réponse, un classement, mais ce classement n'est que l'un de ceux que peut fournir l'individu. Il y a un choix ou une réponse première et souvent, il y a aussi un choix second et même parfois troisième. Le modèle de Coombs affirme que ces seconds choix ou ces seconds classements (ou troisièmes) sont utiles.
[335]

SCHÉMA 9. — Schéma des choix individuels
et de leur dépliage sur une échelle unidimensionnelle
7. L'analyse hiérarchique

Le sociologue autrichien Paul Lazarsfeld qui émigra aux États-Unis mais enseigna aussi à l'École des Hautes Études et à la Sorbonne dit un jour, lorsqu'il dut affronter la tâche de tirer parti d'un matériel très peu systématique mais étendu, que, à condition que l'on disposât de quelque chose, on pouvait toujours en tirer parti, pourvu que l'on eût l'imagination nécessaire. Ceci est inhérent à la situation spécifique de la psychologie sociale, en particulier à celle qui est expérimentale. Et nous ne devrions pas le perdre de vue quand nous avons affaire à certains (pour ainsi dire étranges) projets de recherche, qui peuvent aboutir à quelque chose de tout différent de ce qui était prévu à l'origine. Si la vérité ne se trouve pas sur les rayons d'une bibliothèque, où peut-elle bien se trouver, sinon dans une masse de faits ou d'observations ? N'importe comment, on ne peut s'empêcher de penser que toute échelle est un troupeau de questions posées en vue de dessiner les contours d'une telle masse réelle ou fictive. C'est un fait frappant que les échelles que nous venons de décrire [336] suivent un principe psychophysique et aient été conçues dans le contexte de la psychologie. Les attitudes sociales apparaissent comme un agrégat de jugements et d'évaluations individuels.
Maintenant nous allons décrire l'échelle de Guttman, disciple de Lazarsfeld, qui, elle, emprunte davantage à la sociologie. Son originalité tient à ce qu'elle a trait au contenu des attitudes, des opinions, des représentations sociales, donc à l'échantillonnage des idées et non à l'échantillonnage des individus. Elle suppose un univers d'attitudes propositionnelles, dont un petit nombre sont exprimées par les questions afin de mettre au jour, en quelque sorte, la structure qui les tient ensemble. On aborde donc ces attitudes ou représentations sociales à un niveau social qui se traduit par la redondance des réponses, laquelle signifie qu'elles sont partagées par les membres d'un groupe. Et les erreurs (ou le bruit, ainsi qu'on les nomme dans la théorie de l'information) expriment les réponses qui dévient de la structure mentale ou attitudinale normale. Ce sont donc des patterns d'opinions ou d'attitudes purement individuels (Moscovici, 2000, p. 232). Il faut en tout cas souligner que les attributs, les items, appartiennent à l'univers social et mental « en raison de son contenu. Le chercheur indique le contenu qui l'intéresse par le titre qu'il choisit pour cet univers, et tous les attributs ayant ce contenu se trouvent dans l'univers. (...) Jusqu'ici, l'évaluation de ce contenu peut être décidée par le consensus des juges ou par quelque autre moyen. (...) Il est bien possible que l'analyse formelle du matériel susceptible de former une échelle nous aide à clarifier des régions imprécises du contenu. Cependant, il nous a paru très utile jusqu'à présent d'utiliser l'expérience et le consensus informels dans leur pleine mesure pour définir l'univers » (Guttman, 1944, p. 213).
Cette approche a été utilisée pour la première fois afin d'étudier le moral de l'armée américaine au cours de la Seconde Guerre mondiale. Elle se fonde sur des données mathématiques intéressantes, mais l'on a établi des procédures simples qui ne font pas appel aux statistiques, donc exigent moins de temps pour fournir une bonne image des données. Le mot « image » pourrait être pris ici dans son sens littéral, car les résultats de l'analyse sont facilement présentés sous forme de « scalogramme » qui, d'un seul coup d'œil, renseigne sur la configuration des données qualitatives. C'est pourquoi certains, s'en tenant à cet aspect technique, désignent ce traitement de données par « analyse de scalogramme ». Compte tenu de ses principes théoriques, l'un de nous l'a défini en tant qu' « analyse hiérarchique » (Moscovici, 1954). Ceci parce qu'elle considère toujours une hiérarchie des questions cumulatives à partir de leurs réponses. Ainsi, les trois questions suivante sont cumulatives :
|
1/ Avez-vous une maîtrise en psychologie ?
|
Oui
|
Non
|
|
2/ Êtes-vous bachelier ?
|
Oui
|
Non
|
|
3/ Avez-vous fréquenté l'école primaire ?
|
Oui
|
Non
|
Le sujet qui répond Oui à 1/ doit répondre Oui à 2/ et 3/ ; celui qui répond Non à 2/ ne peut répondre Oui à 1 /, et ainsi de suite. Certes, il s'agit de questions très simples, mais la logique est la même avec des questions plus complexes et dont le critère de hiérarchie est moins évident. Mais ce qu'exprime cette hiérarchie [337] nous apparaîtra plus clairement en proposant un autre exemple pour illustrer le fondement de la démarche de Guttman.
Dans une ville, il y a 70% de taxis de couleur verte et 30% de taxis de couleur bleue. Un individu arrive à une station de taxis et monte dans le premier taxi de la longue file de 7 taxis.
- Q1 : Quelle est la probabilité pour que ce premier taxi soit vert ?
- Q2 : Quelle est la probabilité pour que le premier et le second taxi soient verts ?
- Q3 : Quelle est la probabilité pour que, dans la file de 7 taxis, il y en ait au moins 3 verts ?
Il y a finalement deux possibilités pour étudier les réponses à ces trois questions.
On peut être exhaustif et systématique, ce qui conduit à regarder, pour chaque question, combien de réponses sont justes et combien sont fausses. À chaque question, il y a deux possibilités : soit juste (J), soit faux (F). Les réponses d'un individu donné sont donc une combinaison de ces trois réponses. Par exemple, il peut avoir 3 réponses justes (JJJ) ou il peut avoir juste aux 2 premières et faux à la dernière (JJF) ou encore juste à la première et à la dernière et faux à la seconde (JFJ)...
La combinatoire des deux possibilités de réponses (juste ou faux) à ces 3 questions, montre qu'il y a en tout 8 possibilités.
TABLEAU 12. — Ensemble des combinaisons possibles
|
Q1
|
J
|
F
|
|
Q2
|
J
|
F
|
J
|
F
|
|
Q3
|
J
|
F
|
J
|
F
|
J
|
F
|
J
|
F
|
En fait, toutes ces combinaisons possibles de réponses ne sont pas équiprobables. D est très vraisemblable que certaines combinaisons seront très fréquemment données tandis que d'autres n'apparaîtront peut-être jamais.
La troisième question est plus complexe que la seconde et la seconde question est plus complexe que la première.

SCHÉMA 10. — Degré de complexité des questions
Il est donc vraisemblable que beaucoup d'individus donneront une réponse juste à la première question. Ceux qui répondent faux à cette première question sont tellement nuls en probabilité qu'on voit mal pourquoi ils répondraient juste aux questions suivantes. Par contre ceux qui ont répondu juste à cette première question peuvent répondre juste ou non à la seconde question. Ceux qui donneront une réponse juste à cette seconde question pouvant, éventuellement, s'ils sont très bons en probabilité, donner une réponse juste à la dernière question.
[338]
Donc, si en théorie, il y a bien 8 patterns possibles de réponses, en pratique, seulement 4 devraient apparaître et d'ailleurs indiquer les compétences des individus en matière de probabilité.
TABLEAU 13. — Ensemble des combinaisons vraisemblables
|
|
Très mauvais
|
Mauvais
|
Bons
|
Très bons
|
|
Q1
|
F
|
J
|
J
|
J
|
|
Q2
|
F
|
F
|
J
|
J
|
|
Q3
|
F
|
F
|
F
|
J
|
En fait, il faut connaître la question la plus difficile à laquelle un individu peut répondre pour connaître ses compétences en la matière. S'il répond correctement à une question de complexité de niveau n, il répondra correctement à une autre question de niveau n —1.
Évidemment, ce type de mesure permet simplement d'ordonner les individus, mais il est impossible de dire qu'un individu qui a répondu correctement à 3 questions est trois fois plus compétent que celui qui n'a répondu qu'à la première question. Donc, dans un cas tel que celui-ci, l'étude des connaissances en probabilité, il faut bâtir le questionnaire de telle manière que les réponses des individus s'emboîtent, c'est-à-dire que le phénomène soit scalable, que l'on puisse établir une hiérarchie des réponses.
Nous parlons d'un genre de connaissances qui ont une logique forte. Il est souvent difficile, à propos de ce genre de connaissances, de répondre à la question : pourquoi leur univers forme-t-il une échelle ? Dans un questionnaire, Guttman a posé trois questions portant sur les mathématiques. Elles forment une échelle. Et il s'est demandé : « Pourquoi ces trois questions devraient-elles former une échelle ? Il n'y a pas de raison logique nécessaire expliquant pourquoi une personne doit connaître la surface d'un cercle avant qu'elle puisse savoir ce qu'est une dérivée. La raison pour laquelle une échelle se dégage dans ce cas semble être culturelle » (Guttman, 1944, p. 221). Il est facile - c'est un jeu - de montrer que cela provient de l'éducation, de la séquence selon laquelle on apprend ces matières au lycée. Il ne suffit donc pas de considérer la hiérarchie des questions comme un résultat statistique, il faut encore dégager un aspect sémantique et social.
Mais, pour construire une échelle, il faut suivre trois étapes pratiques. On commence par établir un échantillon d'énoncés (items) à propos des différents attributs de l'objet d'attitude ou de représentation dont on suppose qu'ils appartiennent au même univers par leur contenu. Ensuite, on présente ces énoncés à la population des individus dont on souhaite connaître les réponses. Enfin, connaissant ces réponses, il est possible de savoir si ces énoncés forment une échelle, donc quel est leur ordre, et où se situent les individus les uns par rapport aux autres, donc quel est leur rang.
[339]
- 7.1. Établissement des énoncés

L'élaboration des énoncés ne répond pas à un cheminement strict et mécanique. On sait, qu'à l'arrivée, les bons énoncés constitueront les échelons de l'attitude. Comme dans l'exemple sur la connaissance des probabilités, il faudra que lorsqu'un individu accepte un énoncé, le chercheur puisse savoir, avec suffisamment de certitude, si cet individu a ou non accepté les énoncés qui se trouvent en dessous de cet énoncé. On va donc retenir des énoncés portant sur les différents attributs de l'objet, des énoncés qui permettront de discriminer les niveaux de l'attitude, notamment vers les extrémités et des énoncés dont on peut penser, a priori, que si un individu les accepte, alors, il est très probable qu'il en accepte d'autres. En cela, l'élaboration des énoncés pour l'échelle de Guttman ressemble à l'élaboration d'une échelle de Bogardus, mis à part que, pour Guttman il y aura une phase d'élaboration / validation postérieure au choix des énoncés.
Cette phase d'élaboration/validation postérieure est, en fait, un véritable test d'hypothèse sur la nature de l'attitude vis-à-vis de l'objet et sur les capacités des énoncés à être hiérarchisés.
- 7.2. Établissement de l'échelle

Prenons par exemple 4 énoncés relatifs à un objet (A, B, C, D). On propose ces 4 énoncés à une population de 15 individus et on leur demande si oui ou non ils sont d'accord avec chaque énoncé. On choisit ces 4 énoncés car on suppose qu'ils désignent tous une attitude positive vis-à-vis de l'objet, et on espère qu'ils désignent des niveaux différents de cette attitude.
TABLEAU 14. — Détail des réponses des sujets
(X signifie que l'énoncé a été choisi)
|
Sujets
|
QA
|
QB
|
QC
|
QD
|
|
1
|
|
|
X
|
X
|
|
2
|
|
|
X
|
X
|
|
3
|
X
|
X
|
X
|
X
|
|
4
|
X
|
X
|
X
|
X
|
|
5
|
X
|
X
|
X
|
X
|
|
6
|
|
|
X
|
|
|
7
|
|
|
X
|
X
|
|
8
|
|
|
|
|
|
9
|
|
|
X
|
|
|
10
|
|
|
X
|
|
|
11
|
|
|
X
|
|
|
12
|
X
|
|
X
|
X
|
|
13
|
|
|
X
|
X
|
|
14
|
|
|
|
|
|
15
|
|
|
|
|
[340]
Tableau 15. — Dépouillement des réponses des sujets par question
|
Totaux
|
QA
|
QB
|
QC
|
QD
|
|
X
|
4
|
3
|
12
|
8
|
|
|
11
|
12
|
3
|
7
|
La lecture du simple dépouillement montre que le moins choisi est l'énoncé B suivi du A, suivi du D et suivi du C. Donc, la plupart des individus sont d'accord pour C, mais très peu sont d'accord pour B.
Donc, un premier classement des énoncés peut être effectué sur les états positifs vis-à-vis de l'objet : B X (3), AX (4), D X (8), C X (12).
Si l'on reprend le tableau indiquant le détail des réponses des sujets, qu'on le réorganise et qu'on le trie d'abord sur QB, puis sur QA puis sur QD puis sur QC, on obtient le tableau ci-dessous.
TABLEAU 16. — Détail des réponses des sujets réorganisées et triées
|
Sujets
|
QA
|
QB
|
QC
|
QD
|
|
3
|
X
|
X
|
X
|
X
|
|
4
|
X
|
X
|
X
|
X
|
|
5
|
X
|
X
|
X
|
X
|
|
12
|
|
X
|
X
|
X
|
|
1
|
|
|
X
|
X
|
|
2
|
|
|
X
|
X
|
|
7
|
|
|
X
|
X
|
|
13
|
|
|
X
|
X
|
|
6
|
|
|
|
X
|
|
9
|
|
|
|
X
|
|
10
|
|
|
|
X
|
|
11
|
|
|
|
X
|
|
8
|
|
|
|
|
|
14
|
|
|
|
|
|
15
|
|
|
|
|
La lecture de ce tableau révèle 5 patterns de réponse différents :
- - les sujets 3, 4 et 5 ont choisi tous les énoncés ;
- - le sujet 12 n'a pas choisi QB et a choisi QA, QD et QC ;
- - les sujets I, 2, 7, 13 n'ont pas choisi QB et QA et ont choisi QD et QC ;
- - les sujets 6, 11,9, 10 n'ont pas choisi QB, QA et QD et ont choisi QC ;
- - les sujets 8, 14, 15 n'ont choisi aucun énoncé.
[341]
- 7.3. Évaluation de l’échelle

En fait, ces résultats sont idéaux puisque si un individu choisit QB, il choisit aussi les autres énoncés. S'il choisit QA, il choisit QD et QC. S'il choisit QD, il choisit QC. Il y a donc bien une hiérarchie des énoncés et pour tous les sujets interrogés, ce principe ne souffre pas d'exception.
Ce cas est, bien sûr, assez rare puisque tous les individus ne vont pas établir la même hiérarchie. Il y a presque toujours des erreurs même lors de l'étude de phénomènes dichotomiques évidents comme, par exemple, la mesure de la taille ou du poids d'individus. Normalement, lorsqu'un individu affirme, en réponse à une question, qu'il a une taille supérieure à 1,75 m, il ne devrait pas dire plus loin que sa taille est inférieure à 1,50 m. En effet, une très large majorité d'individus ne donneront pas des réponses aussi incohérentes. Néanmoins, sur un très grand nombre d'interviewés, il n'est pas impossible que de telles erreurs apparaissent, et ceci, d'autant plus qu'on s'éloigne de la mesure de phénomènes évidents et objectifs.
Donc, la lecture du tableau, des réponses des sujets réorganisées et triées, ne sera pas aussi parfaite que celles de nos exemples. Il y aura, dans le tableau, des patterns de réponses s'écartant de la hiérarchie que la majorité des patterns de réponse devrait révéler. La qualité de l'échelle dépend donc de l'émergence d'une structure hiérarchique, des patterns de réponses apparaissant malgré quelques patterns « anormaux » de réponses brouillant la lecture de cette structure.
Imaginons qu'en plus de nos 15 sujets parfaits nous en ayons 3 (le 16, le 17 et le 18) dont les réponses ne s'inscrivent pas exactement dans la hiérarchie définie par les 15 autres sujets.
TABLEAU 17. — Détail des réponses des 18 sujets réorganisées et triées
|
Sujets
|
QA
|
QB
|
QC
|
QD
|
|
|
3
|
X
|
X
|
X
|
X
|
|
|
4
|
X
|
X
|
X
|
X
|
|
|
5
|
X
|
X
|
X
|
X
|
|
|
16
|
X
|
X
|
|
X
|
<---
|
|
12
|
|
X
|
X
|
X
|
|
|
17
|
|
X
|
|
|
<---
|
|
1
|
|
|
X
|
X
|
|
|
2
|
|
|
X
|
X
|
|
|
18
|
|
|
X
|
|
<---
|
|
7
|
|
|
X
|
X
|
|
|
13
|
|
|
X
|
X
|
|
|
6
|
|
|
|
X
|
|
|
9
|
|
|
|
X
|
|
|
10
|
|
|
|
X
|
|
|
11
|
|
|
|
X
|
|
|
8
|
|
|
|
|
|
|
14
|
|
|
|
|
|
|
15
|
|
|
|
|
|
[342]
Les erreurs qui apparaissent remettent-elles en cause la hiérarchie des énoncés ? Pour le savoir, on peut calculer un coefficient de reproductibilité. Dans la vie réelle, il ne faut pas s'attendre à trouver des échelles parfaites. La déviation par rapport à la perfection est mesurée par ce coefficient qui se calcule de la manière suivante :
|
C8 = 1 —
|
nombre d'erreurs
|
|
nombre de questions X nombre de sujets
|
En pratique, des échelles parfaites à 85% ou au-dessus sont considérées comme des approximations efficientes d'échelles parfaites. Ou, en termes de la théorie de l'information (Moscovici et Durain, 1956), on peut parler d'un degré très élevé de redondance de la réponse des individus d'une population. On peut ainsi évaluer à la fois la cohérence interne des questions et l'homogénéité de la population de ceux qui répondent. Ce qui nous donne une idée de l'adéquation de la hiérarchie des questions à la structure de la population.
Cette façon de procéder possède un grand avantage. En effet, une fois l'échelle obtenue, on peut réduire le nombre des questions sans altérer sa valeur de mesure, du moins aussi longtemps que le coefficient de reproductibilité reste le même. Ou encore tant que le degré de redondance et l'homogénéité de la population ne varient pas. C'est-à-dire aussi longtemps que la « normalité sociale » n'est pas modifiée par l'importance des déviations individuelles.
Conclusion

Nous disposons d'une littérature étendue portant sur les échelles. Une partie de ces livres et articles ont trait à leur nature, aux moyens statistiques par lesquels on les définit Une autre partie est consacrée aux recherches effectuées et aux résultats obtenus dans un domaine spécifique (le racisme, par ex.), ou dans une population, ou sur un continent. D'autres encore insistent sur les échecs de la statistique ou critiquent la pertinence de tel ou tel type d'échelle. Par exemple, Festinger (1947) met en doute la pertinence des échelles de Guttman dont les énoncés « sont tous dans une large mesure, des reformulations de la même chose » (p. 155). Ou bien c'est Adorno, le sociologue de l'École de Francfort, qui affirme : « Il est absolument certain que, en tant que construction purement logique d'une méthodologie, ce qu'on appelle l’"échelle de Guttman" est un progrès par rapport aux formes antérieures, et bien plus riche qu'elles. Mais en même temps, ce type d'échelonnage entraîne d'énormes pertes pour ce qui est de la fécondité par rapport à ce qu'on pouvait faire avec des échelles construites sur plusieurs dimensions » (2000, p. 64).
Nous n'allons pas porter la discussion à ce niveau. À coup sûr, il est préférable, avant d'entreprendre une recherche de quelque ampleur scientifique, d'examiner la manière la plus appropriée de s'y prendre. Mais il faut certainement tenir compte des effets de commodité, et aussi des effets de mode. Ainsi, par exemple, l'échelle de Guttman, ou analyse hiérarchique, a relativement peu servi. Elle a fait l'objet d'une [343] « fameuse » dispute, le terme est d'Adorno, et de critiques soutenues. Quelques psychologues sociaux ont néanmoins pris en considération « le progrès par rapport aux formes antérieures » et le fait qu'elle soit « bien plus riche », mais en général, on lui a préféré les autres échelles. Cette abondante littérature reste néanmoins la source inépuisable de nos réflexions. C'est à partir de ces réflexions que nous comprenons mieux leurs principes et fondements psychologiques ou sociaux. En outre, si nous avons besoin d'être guidés sur notre chemin, nous pouvons l'être selon la voie ordinaire des exemples du travail des autres.
Pour rendre notre propos plus précis, nous nous sommes limités aux aspects les plus évidents et les plus pratiques, ou à ceux que nous croyons être tels, de chaque genre d’échelle. En fait, chacune est fondée sur une intuition et quelques procédures qu’un étudiant peut aisément saisir dans le vocabulaire lui-même. Celui qui se préoccupe trop de statistiques avant de maîtriser la méthode elle-même, inverse la démarche naturelle de la recherche. Car il convient de savoir d'abord comment recueillir les données, faire des hypothèses à la lumière d'une théorie, avant d'apprendre à traiter ces données ou à qui les confier dans ce but. Nous avons toujours le temps de voir venir et de prévoir le calcul qu'il faudra, le principal étant d'affiner nos observations et de traiter le matériau linguistique et mental avec une curiosité intellectuelle permanente. Ces rebelles sont donc très importantes, non parce qu'elles nous permettent de mesurer, de laite comme la science, mais parce qu'elles nous permettent défaire de la science.
Références bibliographiques

Adorno T. W., Introduction to Sociology, Stanford (CA), Stanford University Press, 2000.
Bogardus E. S., Measuring social distance, Journal of Applied Sociobgy, 1925, 9, p. 299-308.
Bogardus E. S., A social distance scale, Sociology and Social Research, 1933, Jan-Feb, p. 265-271.
Coombs C. H., Psychological scaling without a unit of measurement, Psychological Review, 1950, 57, p. 145-158.
Coombs C. H., A Theory of Data, New York, Wiley, 1964.
Dawes R. M., Fundamentals of Attitude Measurement, New York, Wiley, 1972.
Dawes R. M. & Smith T. L., Attitude and opinion measurement, in G. Lindzey & E. Aronson (Eds), Handbook of Social Psychobgy, 3rd ed., New York, Random House, 1985, p. 509-566.
Debaly P., La mesure des attitudes, Paris, PUF, 1967.
Festinger L., The treatment of qualitative data by a scale analysis, Psychological Bulletin, 1947, 44, p. 149-161.
Guttman L., A basis for Scaling qualitative data, American Sociological Review, 1944, IX, p. 139-150.
Guttman L., On Festinger's evaluation of scale analysis, Psychological Bulletin, 1947, 44, p. 451-465.
Guttman L., The basis for scalogram analysis, in S. Stouffer, L. Guttman, E. A. Suchman, P. F. Lazarsfeld, S. A. Star & J. A. Clausen, Measurement and Prediction : Studies in Social Psychology in World War II, 4, Princeton, Princeton University Press, 1950, p. 60-90.
Hinckley E. D., The influence of individual opinion on the construction of an attitude scale, Journal of Social Psychology, 1932, 3, p. 283-296.
Hovland G. I. & Sherif M., Judgmental phenomena and the scale of attitude measurement : Item displaeement ou the Thurstone scales, Journal of Abnormal and Social Psychology, 1952, 47. p. 822-832.
[344]
Lemaine J.-M., Initiation aux échelles d'attitudes, Bulletin de psychologie, 1972, no 295, p. 72-101.
Lickert R., A technique for Measurement of Attitudes, Archives of Psychology, 1932, 140, p. 5-53.
Moscovici S., L'analyse hiérarchique, Année psychologique, 1954, 54, p. 83-110.
Moscovici S., Attitudes and opinions, Annual Review of Psychology, 1963, 14, p. 231-260.
Moscovici S., La psychanalyse. Son image et son public, Paris, PUF, 1976.
Moscovici S., Social Representations, Oxford, Polity Press, 2000.
Moscovici S. & Durain G., Quelques applications de la théorie de l'information à la construction des échelles d'attitudes, L'Année psychologique, 1956, 56, p. 47-57.
Reuchlin M., La mesure en psychologie, in P. Fraisse & J. Piaget, Traité de psychologie expérimentale, I. Histoire et méthode, Paris, PUF, 1963, p. 185-221.
Shérif M. & Hovland C. I., Judgmental phenomena and scales of attitude measurement : Placement of items with individual choice of number of categories, Journal of Abnormal and Social Psychology, 1953, 48, p. 135-141.
Stevens S. S. (éd.), Handbook of Experimental Psychology, New York, John Wiley, 1951.
Thomas W. I. & Znaniecki F., The Polish Peasant in Europe and America, Chicago, University of Chicago Press, 1918-1920.
Thurstone L. L., Attitudes can be measured, American Journal of Sociology, 1928, 33, p. 529-554.
Thurstone L. L., Theory of attitudes measurement, Psychological Review, 1929 a, 36, p. 221-241.
Thurstone L. L., Fechner's law and the method of equal appearing intervals, Journal of Experimental Psychology, 1929b, 12, p. 214-224.
Thurstone L. L, & Chave E. J., The Measurement of Attitudes, Chicago, University of Chicago Press, 1929.
* Stéphane Laurent, maître de conférences, Université de Rennes II. Rennes. France.
** Serge Moscovici, directeur d’études, EHESS, Paris, France.
[1] Ce problème de catégorisation est souvent complexe. Par exemple, a priori, la nationalité est une variable nominale. Un individu est soit français, soit espagnol, soit... Néanmoins, il existe des individus ayant une double nationalité. Ils ne peuvent donc pas être affectés à une classe et une seule.
[2] Ces distances se calculent sur des jugements de comparaison par paires, elles indiquent donc des distances entre deux énoncés, mais il n'est pas possible d'additionner, par exemple, des distances obtenues sur deux paires différentes. Ceci n'est pas une échelle d'intervalle, donc l'égalité suivante : DAC = DAB + DBC n'a pas de sens ici. De toute façon, les comparaisons ayant été faites sur des paires différentes, il faut supposer que chaque paire apporte avec elle sa mesure propre, donc on ne peut pas ajouter ou soustraire de distances provenant de mesures différentes.
|

